感知机

感知机

感知器假设集（Perceptron Hypothesis Set）

感知器算法: \(h(x)=sign((\sum_{i=1}^dw_ix_i)-threshold)\)

对上面的公示进行变形，将threshold作为偏置，纳入 x 中，\(x_0=+1\) ;

\[h(x)=sign(W^TX)\]

每一个不同的W代表了算法中的一个hypothesis.

PLA 感知器学习算法

要从 hypothesis set 中找到一个合适的 hypothesis g, 让 g 与目标函数 f 尽可能的相近。

PLA算法通过试错的方法实现模型的训练：

总共进行t轮的训练， t=0, 1, …

随机初始化 \(w_0\);
将样本 \((x_{n(t)},y_{n(t)})\) 带入PLA学习机，如果：

\[sign(w^T_tx_{n(t)})\neq y_{n(t)}\]

那么，表示发生错误，需要对错误进行纠正。

修正错误：
\[w_{t+1} \leftarrow w_t + y_{n(t)}x_{n(t)}\]
\(w\): 代表分类线的法向量 \(x_n\): 是原点到 \(x_n\) 的向量

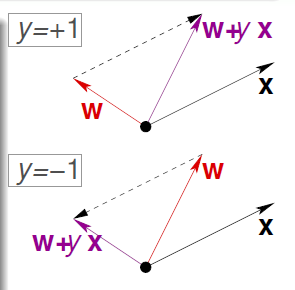
当 \(y_n = +1\), 将 \(w\) 的方向向样本 \((x_n, y_n)\) 的方向转动。
当 \(y_n = -1\), 将\(w\)的方向向样本 \((x_n, y_n)\) 的反方向转动。
当不再出现错误的时候，训练结束。

PLA算法要能终止，要求训练数据集必须是线性可分的

\(w_t\) 越来越接近 \(w_f\)

\(w_f\): 目标函数 f 对应的参数，因此对于任意一个样本，它都能正确的分类：
\[y_{n(t)}w^T_fx_{n(t)} \ge \min_ny_nw^T_fx_n \gt 0\]
衡量两个向量是否接近，可以用它们的内积，如果内积越小代表它们越不接近，相互垂直时为 0
\[\begin{align} \begin{split} w_f^Tw_{t+1} &= w_f^T(w_t+y_{n(t)}x_{n(t)}) \\ &\ge w_f^Tw_t + \min_ny_nw_f^Tx_n \\ &\gt w_f^Tw_t + 0 \end{split} \end{align}\]

\(w_t\) 的增长速率不快

\(w_t\)每次的更新不超过离分割线最远的样本的距离

\(w_t\) 的每次更新发生在有错误的时候：

\[sign(w_t^fx_{n(t)}) \neq y_{n(t)} \Leftrightarrow y_{n(t)}w_t^Tx_{n(t)} \leq 0\]

对于每一次更新后的结果：

\[\begin{equation}\begin{split} ||w_{t+1}||^2 &= ||w_t + y_{n(t)}x_{n(t)}||^2\\\\ &= ||w_t||^2 + 2y_{n(t)}w_t^Tx_{n(t)} + ||y_{n(t)}x_{n(t)}||^2\\\\ &\le ||w_t||^2 + 0 + ||y_{n(t)x_{n(t)}}||^2\\\\ &\le ||w_t||^2 + \max_n||y_{n(t)}x_{n(t)}||^2\end{split}\end{equation}\]

其中 \(\max_n \Vert y_{n(t)}x_{n(t)} \Vert ^2\) 就代表了距离到分隔线最远的点的距离。

\[\begin{equation}\begin{split} \text{start from w_0 = 0, after T mistake corrections,} \\ \frac{w_f^T}{\Vert w_f \Vert} \frac{w_T}{\Vert w_T \Vert} \ge \sqrt T * \text{constant} \end{split}\end{equation}\]

\(w_f^Tw_{t+1}\) 的内积是小于等于1的，再根据上面的式子，知道T不可能为无穷大，所以运算会终止。

Pocket 算法

算法步骤

随机初始化 w
进行 t 轮的学习， t = 0, 1, …
如果发生错误，按照 PLA 算法对 w进行纠正：\(w_{t+1} \leftarrow w_t + y_{n(t)}x_{n(t)}\)
判断对比纠正后的算法与之前算法的错误率，如果更好，者保留新的w_t+1, 否者保留之前的w。
运算足够多次之后停止运算。

Pocket算法是PLA的改进算法，用于解决线性不可分的数据集。 Pocket算法的运算量大：对于比PLA，在得到新的w_t+1，需要将所有数据集运算一遍，来获得错误率。