机器学习中的交叉熵
机器学习中的交叉熵
交叉熵损失函数是机器学习分类问题中最常用的一个损失函数。但是很多人对于“交叉熵”的概念缺乏理解。本文的目的是希望能够通俗易懂的解释清楚 “熵”, “交叉熵” 和 “KL-散度” 这三个相关的概念。
信息论中的“熵”
“熵” (entropy) 这个概念在热力学中表示一个系统的无序程度,熵越大系统就越混乱。1948年香农在其发表的《通信的数学理论》论文中给出了”信息熵“的定义:信息熵是随机事件不确定性的度量。信息熵与热力学熵有着紧密的内在联系,不过在本文中所讨论的熵都是指信息熵。
有效信息长度
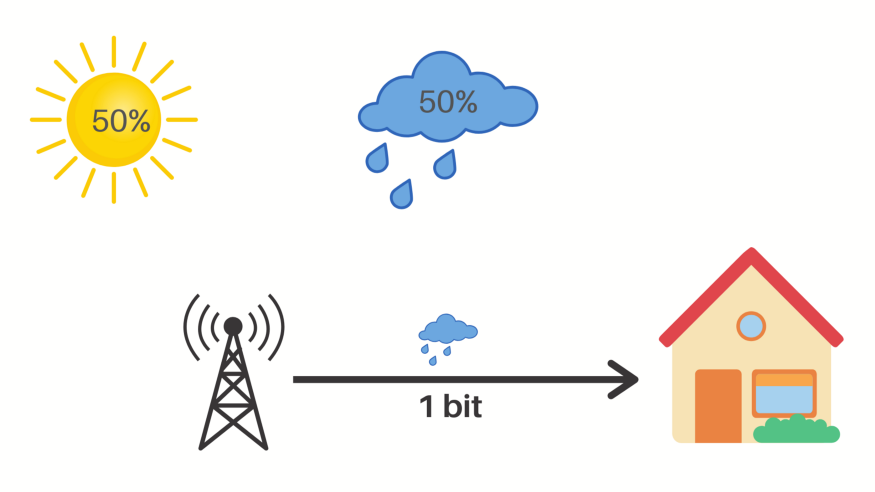
为了能更好的解释信息熵,我们先来看一个例子。有一个气象监测站,通过检测某地的气象数据,能给出第二天的天气预测。气象站需要将预测结果网络发送给气象中心。如果当地只有两种天气一种是晴天,一种是雨天,那么气象站如何能够高效的发送预测结果呢?最简单的情况下,气象站可以将预测结果以汉字的形式发送出去。如果预测是晴天就发送”晴天“,如果是雨天就发送”雨天“。我们知道一个汉字在计算机中通常的编码长度是 2 byte,也就是 8 bit,那么这两个汉字就是 16 bit。为了能更高效的发送信息,我们可以对信息进行编码,用 0 来表示晴天,1 来表示雨天。那么我们需要发送的信息长度就只有 1 bit 了。对于原来长度为 16 bit 的信息来说,它真正有效的信息长度其实只有 1 bit。
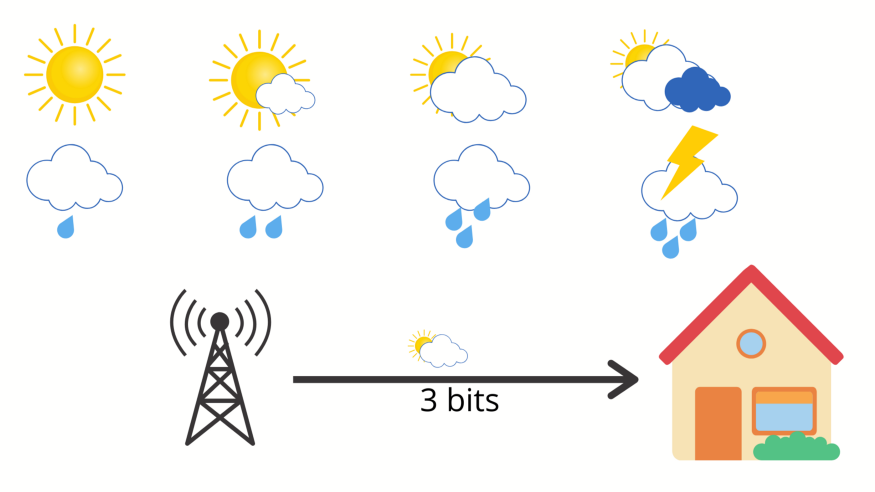
那如果当地天气有8种情况,我们需要多少长度的消息才能发送预测结果呢?答案很简单:\(2^3=8\) ,我们只需要3个 bit 就能发送8种天气。在计算机中对于任意n种分类情况,我们只需要 \(log_2 (n)\) 长度的编码信息就可以把所有的情况进行编码。
信息熵
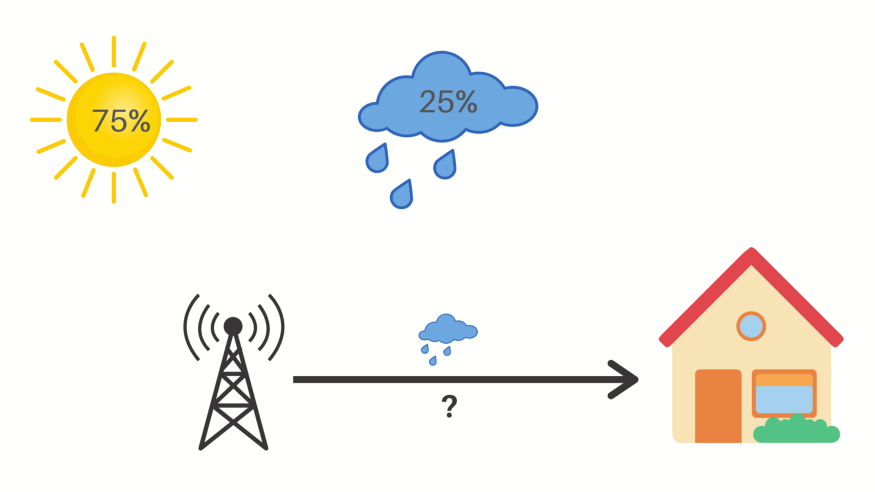
我们知道在现实中,第二天出现什么天气的概率不是均等的,在夏天出现晴天和雨天的概率比较大,而出现雪天的概率很小;而在冬天出现雨天的概率较小,出现雪天的概率较大。在第一个例子中如果晴天的概率是 75%, 雨天的概率是 25%,那么消息的长度应该是多少呢?在计算消息长度之前,我们需要先介绍“熵减因子”(reduction factor)的概念。按照香农在论文中提出:
每发送1个bit的有效信息,能减少了接收者2个因子的不确定性。
熵减因子 m 与有效消息长度 u 之间的关系是: \(2^u=m\)
在已知事件概率的情况下,熵减因子 m 与概率 p 的关系是: \(\frac{1}{p}=m\)
基于熵减因子与概率的关系,我们可以根据概率 p 推断出有效信息的长度 u 的关系: \(-log_2{p} = u\)
现在我们可以回答之前提出的问题了。
晴天的有效信息长度 \(m_s = -log_2{p_s} = -log_2{0.75} = 0.41\)
雨天的有效信息长度 \(m_r = -log_2{p_r} = -log_2{0.25} = 2\)
平均有效信息长度 \(m_{avg} = p_s * (-log_2{p_s}) + p_r * (-log_2{p_r}) = 0.75 * 0.41 + 0.25 * 2 = 0.81\)
平均有效信息长度又被称为信息熵 , 数学定义为:
\[\text{Entropy},H(p) = - \sum{p(i)*log(p(i))}\]我们按照现实情况,分别给第二个例子中8种天气加一个概率。
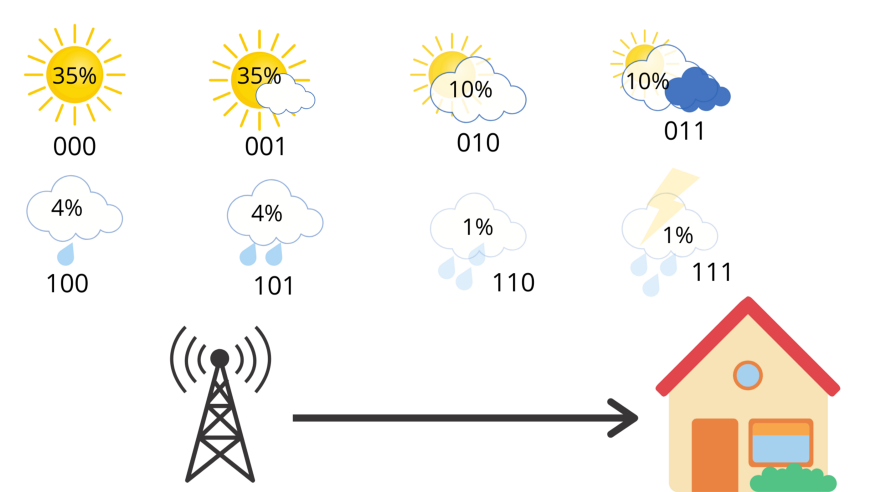
按照信息熵的定义,我们可以计算出此时的信息熵:
\[\begin{aligned} \text{Entropy} & = -0.35 * log_2{0.35} -0.35 * log_2{0.35} \\ & -0.10 * log_2{0.10} -0.10 * log_2{0.10} \\ & -0.04 * log_2{0.04} -0.04 * log_2{0.04} \\ & -0.01 * log_2{0.01} -0.01 * log_2{0.01} \\ & = 2.23 \end{aligned}\]信息熵是理论上最小的平均消息长度。
交叉熵
通过信息熵公式我们可以计算出,理论上发送信息的最小平均长度是 2.23,上图因为多所有天气都按照3位进行编码,所以消息的平均长度是3。通过修改信息的编码方式,我们可以降低消息的平均长度。
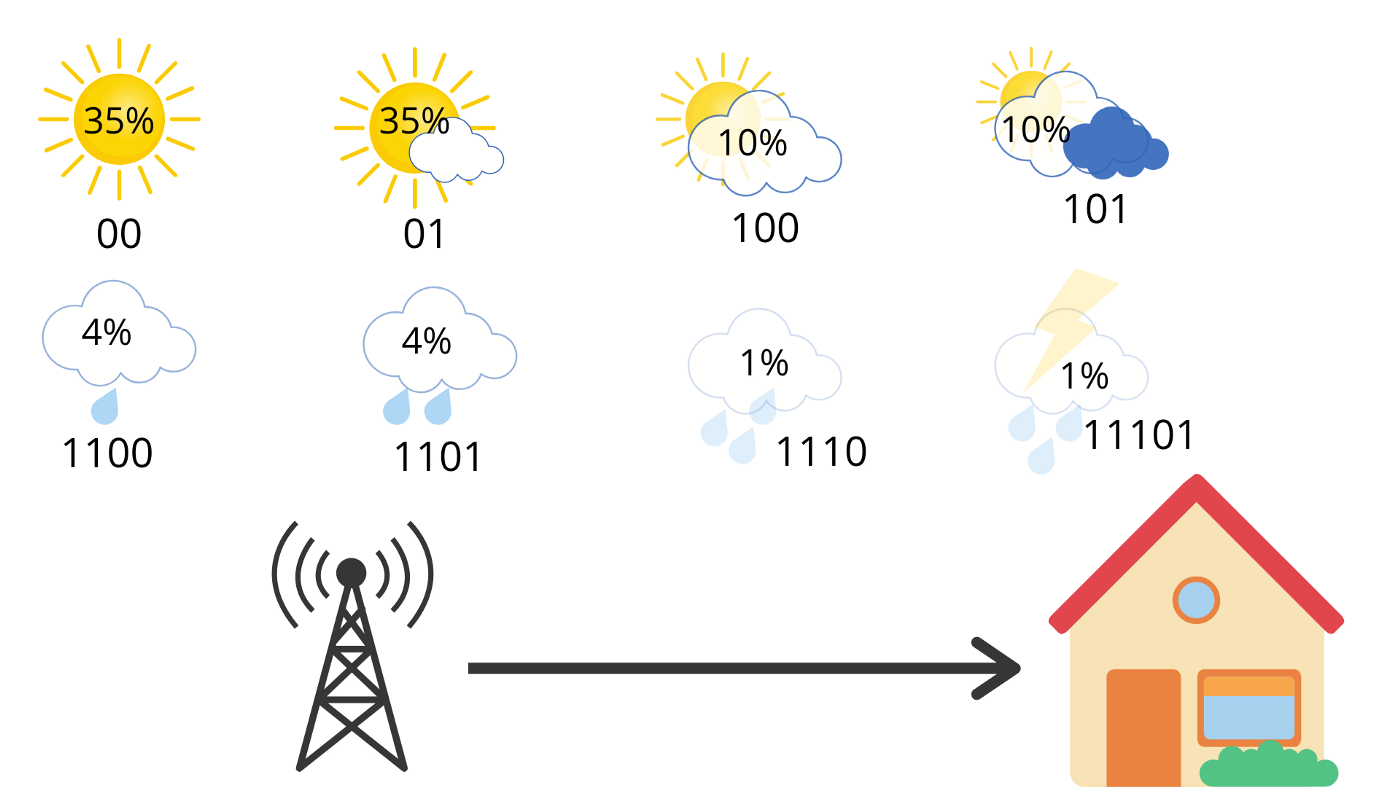
通过减小高概率天气的消息长度,增长低概率天气的消息长度,我们可以降低平均的消息长度。
\(0.35 * 2 + 0.35 * 2 + 0.1 * 3+ 0.1 * 3 + 0.04 * 4 + 0.04 * 4 + 0.01 * 4 + 0.01 * 5 = 2.42\)
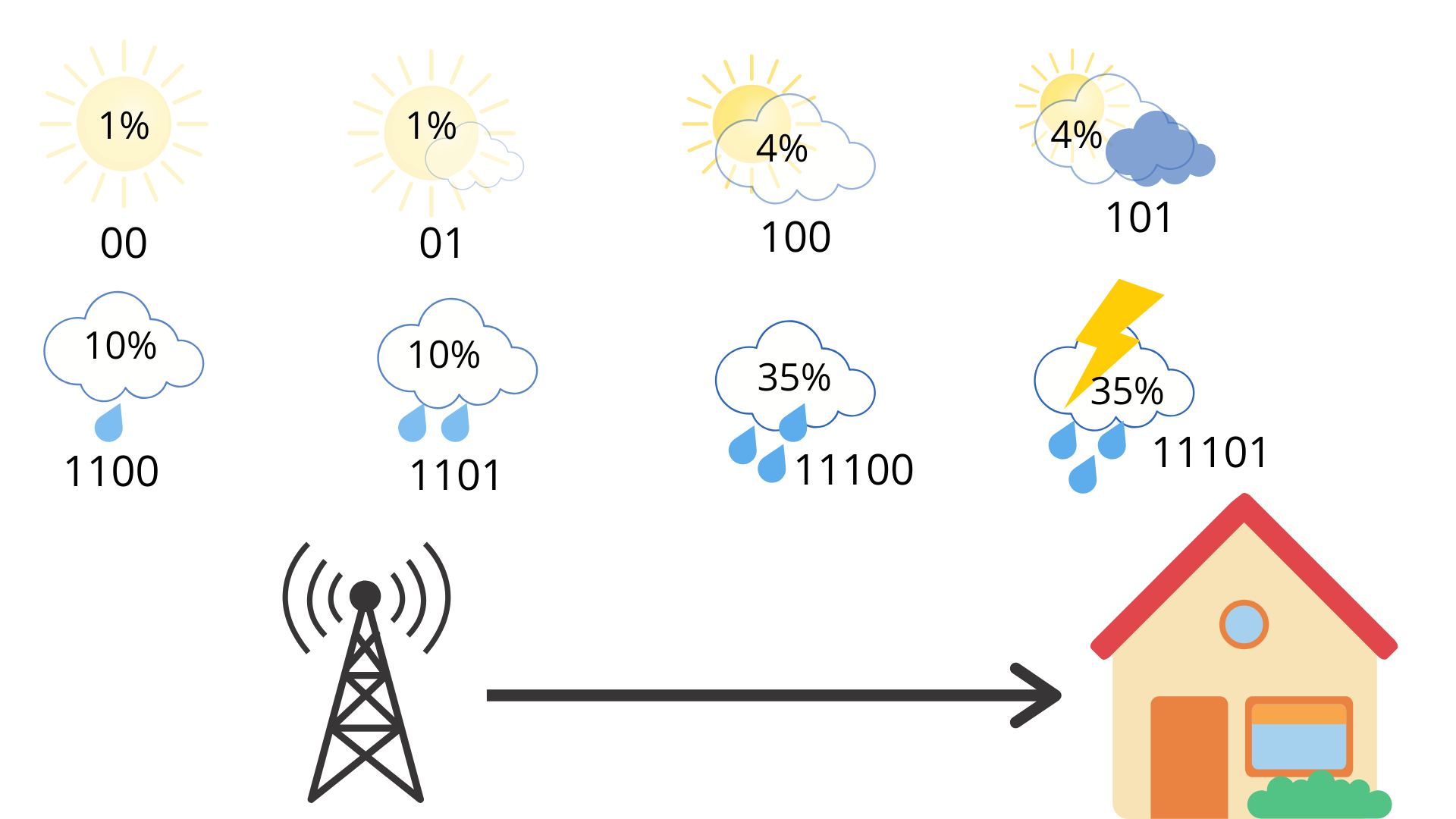
如果我们反过来增长低概率天气的消息长度,减小大概率天气的长度,那么消息的平均长度增大。 \(0.01 * 2 + 0.01 * 2 + 0.04 * 3 + 0.04 * 3 + 0.1 * 4 + 0.1 * 4 + 0.35 * 5 + 0.35 * 5 = 4.58\)
上面两个例子中,我们计算信息平均长度时,是用真实的天气概率乘以我们给定的有效信息长度, 上面计算结果叫做交叉熵。
在已知各种情况天气的概率下,可以通过信息熵的公式计算出理论上最小的平均信息长度。但是在现实生活中,我们经常是不知道各种情况的实际概率分布的。在这种情况下,我们可以预先给出一个对于真实概率分布的一个估计(在上面的例子是预先给出一个信息长度)。
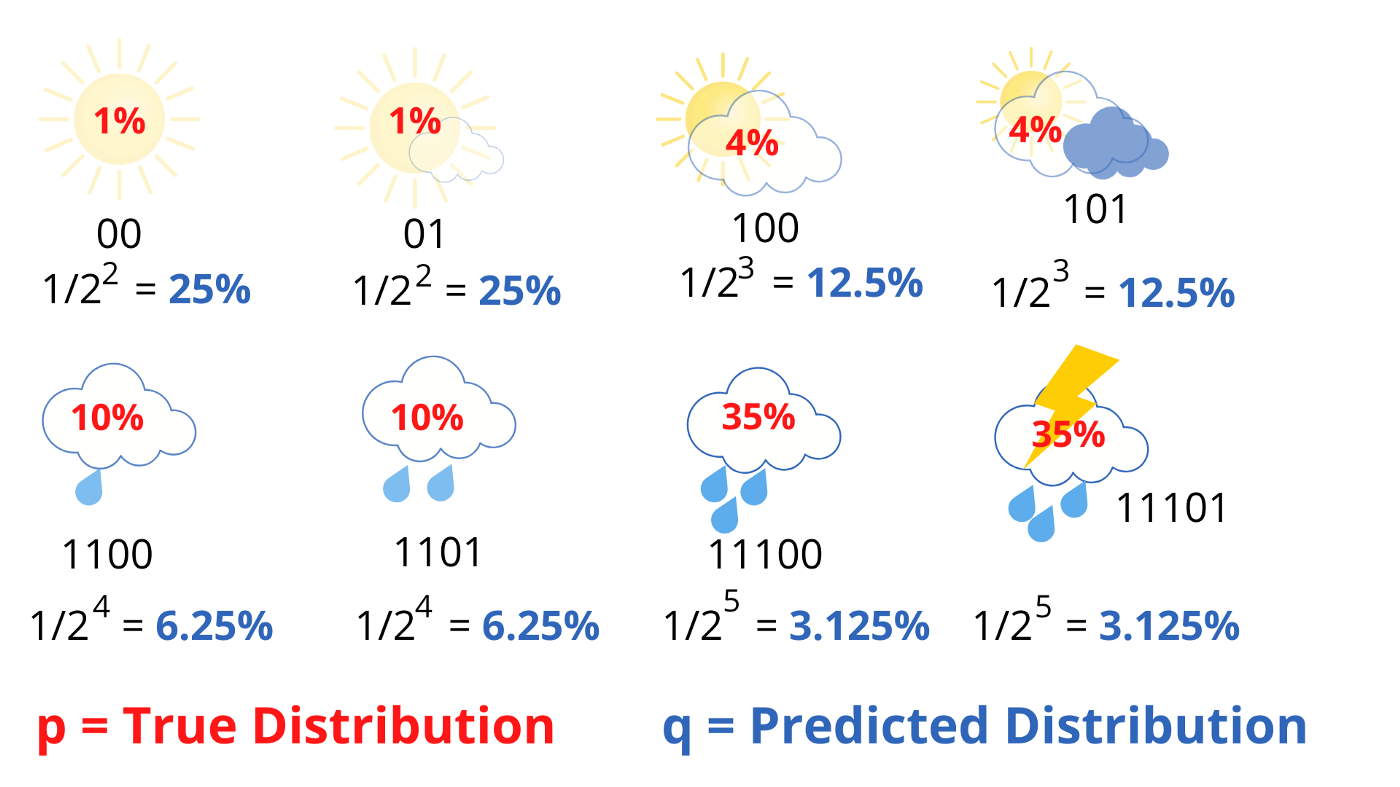
图中红色的概率代表天气的真实分布,而蓝色概率代表按照编码长度推算出来的对于天气概率的估计。真实的概率分布于估计概率分布之间的关系可以用交叉熵的形式表达出来。
\[\text{CrossEntropy,}H(p,q) = - \sum{p(i)log(q(i))}\]通过前面的内容我们可以知道,只有估计概率越接近于真正的概率,交叉熵才会越小,当估计概率等于真实概率时,交叉熵等于信息熵。
交叉熵公式于信息熵公式的不同之处在于,将 log 部分的概率分布替换成了预测概率分布。交叉熵大于信息熵的部分叫做Kullback-Leibler Divergence(KL散度)也叫相对熵(Relative Entropy)。
\[\begin{aligned} \text{KL-Divergence} &= \text{Entropy} - \text{CrossEntropy} \\ D_{KL}(p||q) & = H(p,q) - H(p) \\ & = -\sum_i{p_ilog(q_i)} - (-\sum_i{p_ilog(p_i)}) \\ & = -\sum_i{p_ilog(q_i)} + \sum_i{p_ilog(p_i)} \\ & = \sum_i{p_i log(\frac{p_i}{q_i})} \end{aligned}\]交叉熵在机器学习中的应用
由于交叉熵的性质,所以在机器学习中,交叉熵被广泛的作为分类损失函数。
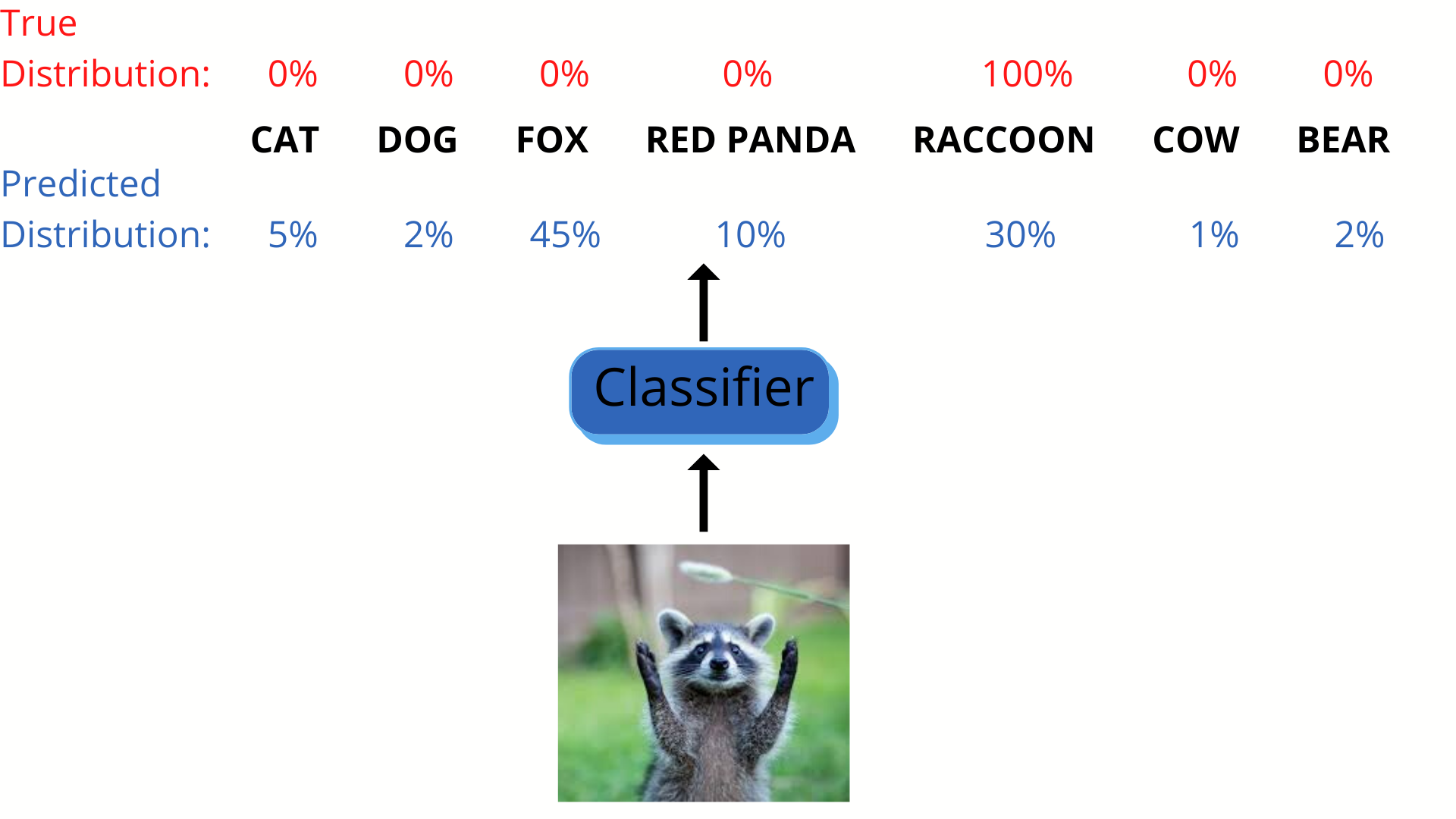
在一个分类任务的训练过程中,我们已知目标的真实概率分布,分类器在每次的训练过程中会给出一个预测的概率分布。我们把交叉熵作为我们的目标函数,优化的方向是使得目标函数(交叉熵)最小,交叉熵只有在预测概率分布于真实概率分布一致的情况下最小,所以交叉熵非常适合作为分类任务的损失函数。
在信息论中信息熵,交叉熵公式中的 log 都是以 2 为底的对数,但是在机器学习中代码实现中,无论是用以10为底或者e为底都无所谓,因为对数都可以通过换底公式进行变换: \(log_e{n} = \frac{log_2{n}}{log_2{e}}\) ,因为分母始终是一个常数所以对于损失函数没有影响。
信息熵原本作为信息论的一个重要概念,没有想到在多年以后会在机器学习中继续大放异彩。希望通过本文的内容能理解交叉熵损失函数真正的意义。本文是根据文章 Entropy, Cross-Entropy, and KL-Divergence Explained! 进行的改写,读者可以阅读原文获得跟多关于交叉熵的认识。